Notes About

Deep Clustering

Can deep neural networks learn to do clustering? Introduction, survey and discussion of recent works on deep clustering algorithms.

Massive amount of data is generated everyday. Although supervised learning has been at the core of recent success of deep learning, unsupervised learning has the potential to scale with this ever increasing availability of data as it alleviates the need to carefully hand-craft and annotate training datasets.

Clustering is one of the fundamental unsupervised method of knowledge discovery. It’s goal is to group similar data points together without supervision or prior knowledge of nature of the clusters. Various aspects of clustering such as distance metrics, feature selection, grouping methods etc. have been extensively studied since the origin of cluster analysis in the 1930s. Because of it’s importance in exploratory understanding of data, clustering has always been an active field of research.

Galvanized by the widespread success of deep learning in both supervised and unsupervised problems, many of the recent work on clustering has been focused on using deep neural networks-often, this pairing is commonly referred to as deep clustering.

Deep Clustering Framework

Deep clustering algorithms can be broken down into three essential components: deep neural network, network loss, and clustering loss.

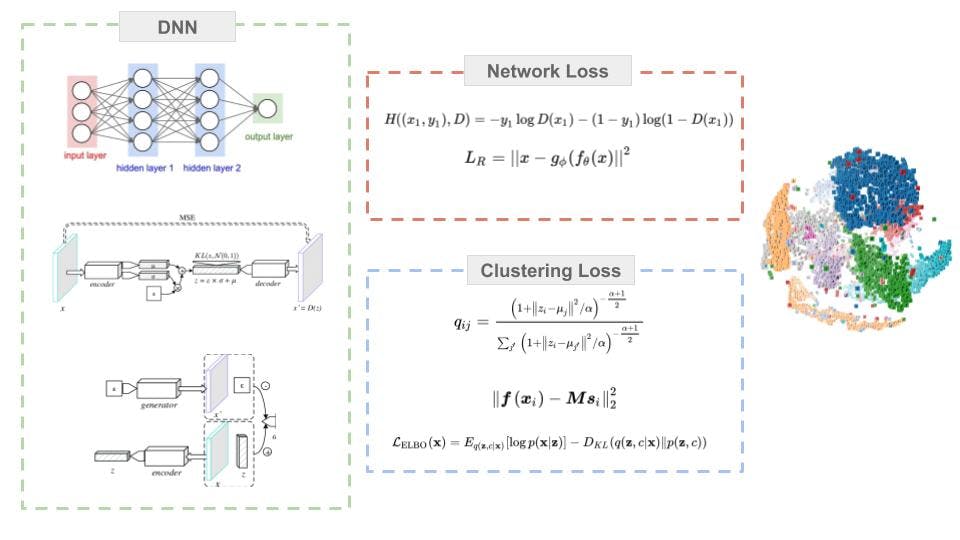
Deep Neural Network Architecture

The deep neural network is the representation learning component of deep clustering algorithms. They are employed to learn low dimensional non-linear data representations from the dataset. Most widely used architectures are autoencoder based, however generative models like Variational Autoencoders and Generative Adversarial Networks have also been used in different algorithms. Variations in network architecture like convolutional neural networks are also widely used.

Loss Functions

The objective function of deep clustering algorithms are generally a linear combination of unsupervised representation learning loss, here referred to as network loss \(L_R\) and a clustering oriented loss \(L_C\). They are formulated as

\[L = \lambda L_R + (1-\lambda) L_C\]

where \(\lambda\) is a hyperparameter between 0 and 1 that balances the impact of two loss functions.

Network Loss

The neural network loss refer to the reconstruction loss of autoencoder, variational loss of VAEs, or the adversarial loss of GANs. The network loss is essential for the initialization of the deep neural networks. Usually after a few epochs, the clustering loss is introduced by changing the \(\lambda\) hyperparameter.

Some models like JULE, DAC and IMSAT discard the network loss altogether in favour of just using clustering loss to guide both representation learning and clustering.

Clustering Loss

Several different clustering loss has been proposed and used in different algorithms. They can be generally categorized into:

  1. Cluster Assignment

    Cluster assignment losses provides cluster assignments to the data points directly, and no further clustering algorithm is required to be run on top the learnt data representations. Some examples are: k-means loss , cluster assignment hardening loss and agglomerative clustering loss.

  2. Cluster Regularization

    Cluster regularization loss, on the other hand, only enforces the network to preserve suitable discriminant information from the data in the representations. Further clustering on the representation space is necessary to obtain the clustering result. Some examples are: locality preserving loss, group sparsity loss etc.

Performance Metrics

In deep clustering literature, we see the regular use of the following three evaluation metrics:

  1. Unsupervised Clustering Accuracy (ACC)

    ACC is the unsupervised equivalent of classification accuracy. ACC differs from the usual accuracy metric such that it uses a mapping function \(m\) to find the best mapping between the cluster assignment output \(c\) of the algorithm with the ground truth \(y\). This mapping is required because an unsupervised algorithm may use a different label than the actual ground truth label to represent the same cluster. A reference python implementation can be found here.

\[ACC = max_{m} \frac{\sum_{i=1}^n1\{y_i = m(c_i)\}}{n}\]

  1. Normalized Mutual Information (NMI)

    NMI is an information theoretic metric that measures the mutual information between the cluster assignments and the ground truth labels. It is normalized by the average of entropy of both ground labels and the cluster assignments. Sklearn’s implementation is available as sklearn.metrics.normalized_mutual_info_score.

\[NMI(Y,C) = \frac{I(Y,C)}{\frac{1}{2}[H(Y)+H(C)]}\]

  1. Adjusted Rand Index (ARI)

    The Rand Index computes a similarity measure between two clusterings by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in the predicted and true clusterings. The adjusted Rand index is the corrected-for-chance version of the Rand index. Sklearn’s implementation is available as sklearn.metrics.adjusted_rand_score.

Current Approaches on Deep Clustering

Based on the different network architectures and the nature of loss functions used, we can broadly categorize current deep clustering models into following three categories:

AutoEncoders based

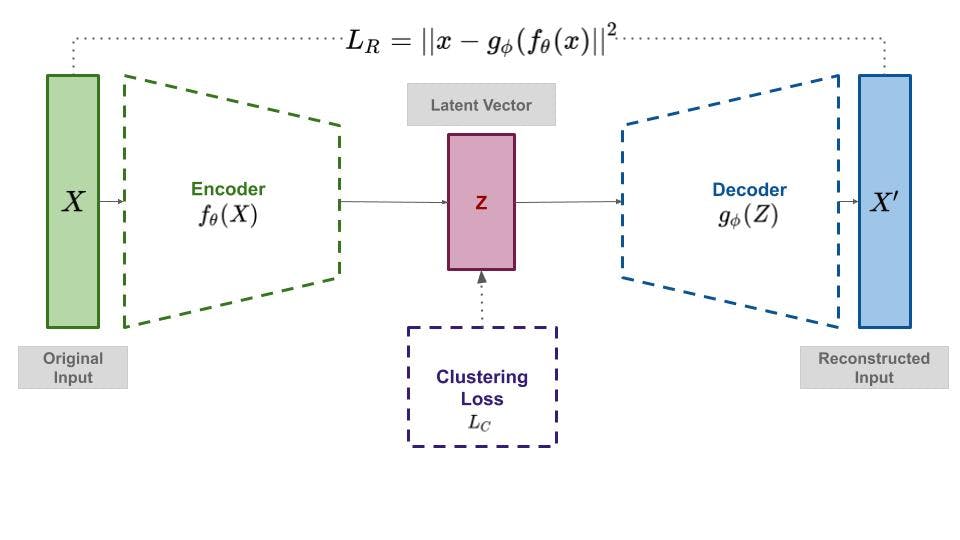
Autoencoders have found extensive use in unsupervised representation learning tasks ranging from denoising to neural machine translation. The simple yet very powerful framework is also used extensively in deep clustering algorithms.

Most of the AE based deep clustering approaches use a pre-training scheme in which the encoder and decoder network parameters are initialized with the reconstruction loss before clustering loss is introduced.

Learning Embedding Space for Clustering From Deep Representations [paper] [code] [colab]

Autoencoders learn a low dimensional manifold of data generating distribution. But the representation space is compact and has severe overlapping between the clusters.

In order to separate out the clusters, the representation space should be regularized so that sub manifolds of the classess are separated well. But this comes at a cost of corrupting the feature space and so the reconstruction capacity of the decoder suffers.

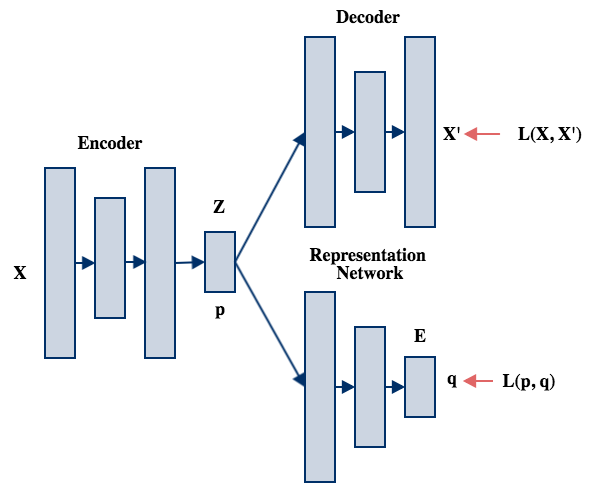
One way to circumvent this tradeoff is to use a different representation space termed embedding space E which is learned by a Representation network from the latent space Z of the encoder. This network is inspired by parametric-tsne.

First the pairwise probabillity p denotes the probability of two points lying together in the encoded space Z is calculated using Student’s t-distribution kernel:

\[p_{ij} = \frac{(1+||f(x_i)-f_(x_j)||^2/\alpha)^{-\frac{\alpha+1}{2}}}{\sum_{k\neq l }(1+||f(x_k)-f(x_l)||^2/\alpha)^{-\frac{\alpha+1}{2}}}\]

Student’s t distribution is used because it approximaes Gaussian distribution for higher degree of freedoms, and doesn’t have kernel width parameter. It also assigns stricter probabilities. The degree of freedom is taken as 2 times the dimension of Z which allows more space to model the local structure of the representation space.

Similarly, pairwise probability q denotes probability of two points lying together in embedding space E.

\[q_{ij} = \frac{(1+||h(z_i)-h(z_j)||^2)^{-1}}{\sum_{k\neq l }(1+||h(z_k)-h(z_l)||^2)^{-1}}\]

Here degree of freedom is chosen as 1 which limits the freedom to model the local structure, and thus distribution approaches p by minimization of KL divergence by creating strong repulsive force between clusters.

The Representation Network is trained by cross entropy of p and q, which has the effect of minimizing the entropy of distribution p as well.

This paper achieved SOTA results in Reuters News dataset for clustering accuracy.

Clustering Accuracy (ACC):

Deep Embedded Clustering (DEC) [paper] [code]

Deep Embedded Clustering is a pioneering work on deep clustering, and is often used as the benchmark for comparing performance of other models. DEC uses AE reconstruction loss and cluster assignment hardeining loss. It defines soft cluster assignment distribution \(q\) based on Student’s t-distribution with degree of freedom \(\alpha\) set to 1. To further refine the assignments, it also defines an auxiliary target distribution derived from this assignment \(p_{ij}\), which is updated after every \(T\) iterations.

\[q_{i j}=\frac{\left(1+\left\|z_{i}-\mu_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|z_{i}-\mu_{j^{\prime}}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}\] \[p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}}\]

The training begins with a pre-training stage to initialize encoder and decoder parameters for a few epochs with reconstruction loss. After pre-training, it removes the decoder network and the encoder network is then fine-tuned by optimizing KL divergence between soft cluster assignment \(q_{ij}\) and auxilliary distribution \(p_{ij}\). This training can be thought of as a self-training process to refine the representations while doing cluster assignment iteratively.

\[\min \sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}}\]

Clustering Accuracy (ACC):In this article only ACC of the models are reported as not all papers report NMI or ARI.

Discriminately Boosted Clustering (DBC) [paper]

Discriminately Boosted Clustering builds on DEC by using convolutional autoencoder instead of feed forward autoencoder. It uses the same training scheme, reconstruction loss and cluster assignment hardening loss as DEC. DBC achieves good results on image datasets because of its use of convolutional neural network.

Clustering Accuracy (ACC):

Deep Clustering Network (DCN) [paper] [code]

Deep Clustering Network utilizes an autoencoder to learn representations that are amenable to the K-means algorithm. It pre-trains the autoencoder, and then jointly optimizes the reconstruction loss and K-means loss with alternating cluster assignments. The k-means clustering loss is very intuitive and simple compared to other methods. DCN defines it’s objective as:

\[\min \sum_{i=1}^{N}\left(\ell\left(\boldsymbol{g}\left(\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right), \boldsymbol{x}_{i}\right)+\frac{\lambda}{2}\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2}\right)\]

where \(\boldsymbol{f}\) and \(\boldsymbol{g}\) are encoder and decoder functions respectively, \(s_i\) is the assignment vector of data point \(i\) which has only one non-zero element and \(M_k\), denotes the centroid of the \(k\)th cluster.

Clustering Accuracy (ACC):

Deep Embedded Regularized Clustering (DEPICT) [paper] [code]

Deep Embedded Regularized Clustering consists of several tricks. It uses softmax layer stacked on top of convolutional autoencoder with a noisy encoder. It jointly optimizes reconstruction loss and cross entropy loss of softmax assignments and it’s auxilliary assignments which leads to balanced cluster assignment loss. All the layers of the encoder and decoder also contribute to the reconstruction loss instead of just input and output layers.

\[p_{i k}=\frac{\exp \left(\boldsymbol{\theta}_{k}^{T} \mathbf{z}_{i}\right)}{\sum_{k^{\prime}=1}^{K} \exp \left(\boldsymbol{\theta}_{k^{\prime}}^{T} \mathbf{z}_{i}\right)}\] \[q_{i k}=\frac{p_{i k} /\left(\sum_{i^{\prime}} p_{i^{\prime} k}\right)^{\frac{1}{2}}}{\sum_{k^{\prime}} p_{i k^{\prime}} /\left(\sum_{i^{\prime}} p_{i^{\prime} k^{\prime}}\right)^{\frac{1}{2}}}\] \[\min -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} q_{i k} \log p_{i k}\]

DEPICT achieves very impressive clustering performance as a result of these improvements.

Clustering Accuracy (ACC):

Generative Model Based

Generative models like Variational Autoencoders and Generative Adversarial Networks learn latent representation space that can be interpolated to generate new samples from the data distribution.

Variational Deep Embedding (VaDE) [paper] [code]

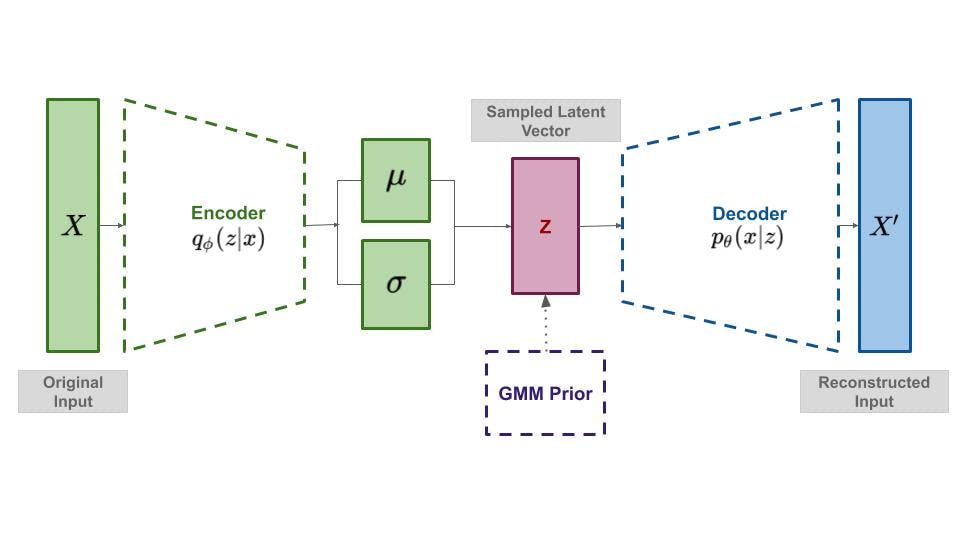
VaDE incorporates probabilistic clustering problem within the framework of VAE by imposing a GMM prior over VAE. The optimization essentially minimizes reconstruction loss and KL divergence between Mixture of Gaussians prior \(c\) to the variational posterior to learn a uniform latent space with clusters which allows interpolation to generate new samples.

\[\mathcal{L}_{\mathrm{ELBO}}(\mathbf{x})=E_{q(\mathbf{z}, c | \mathbf{x})}[\log p(\mathbf{x} | \mathbf{z})]-D_{K L}(q(\mathbf{z}, c | \mathbf{x}) \| p(\mathbf{z}, c))\]

After the optimization, the cluster assignments can be inferred directly from the MoG prior. One strong advantage of VaDE is that it stands on the strong theoretical ground of VAE.

Clustering Accuracy (ACC):

Information Maximizing Generative Adversarial Network (InfoGAN) [paper] [code]

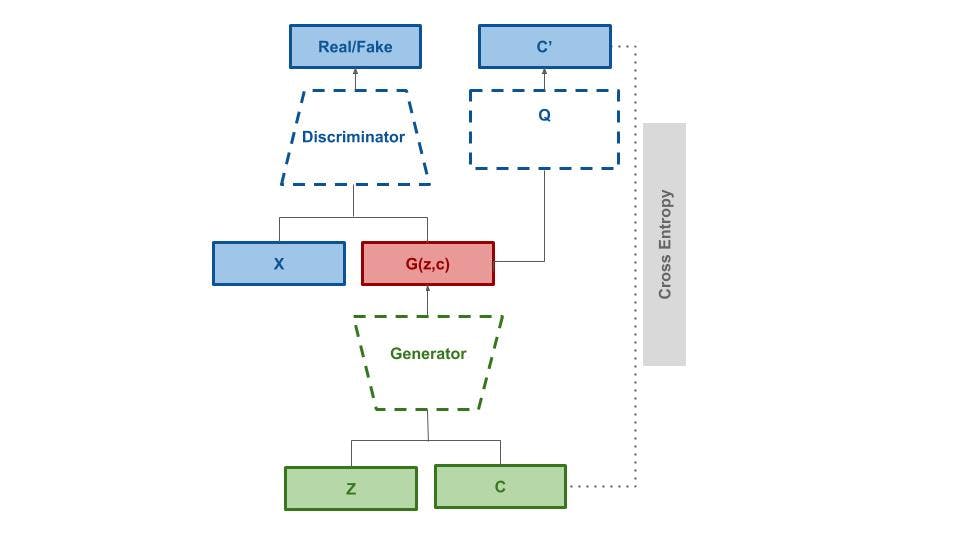
Another generative approach towards clustering is InfoGAN. It’s primary objective is to learn disentangled representations. InfoGAN decomposes the input into two parts: incompressible noise \(z\) and latent code \(c\), so the form of the generator becomes \(G(z, c)\). It then combines standard GAN objective with information-theoretic regularization \(I(c; G(z, c))\). When choosing to model the latent codes with one categorical code having k values, and several continuous codes, it has the function of clustering data points into k clusters.

\[\min _{G} \max _{D} V_{I}(D, G)=V(D, G)-\lambda I(c ; G(z, c))\]

Direct Cluster Optimization

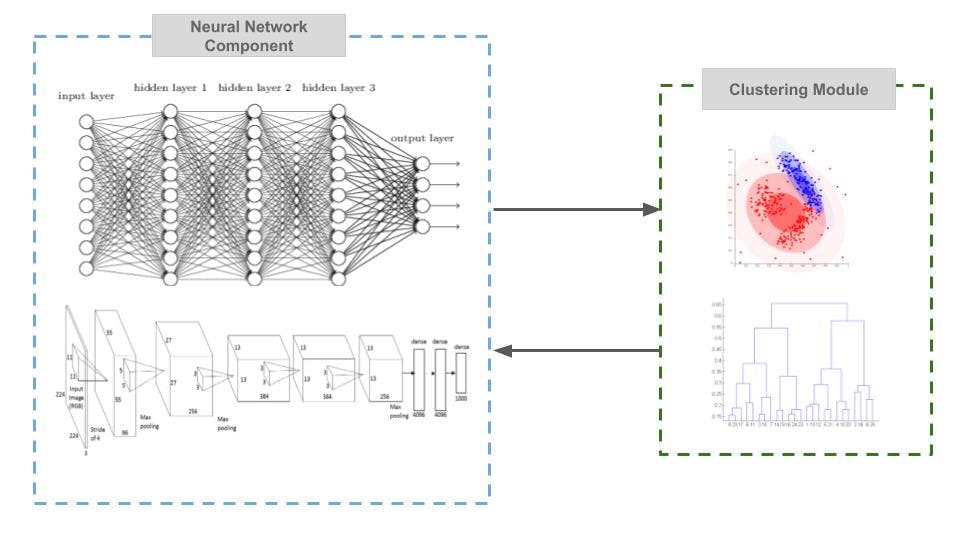
The third category of deep clustering models discard any reconstruction loss and use clustering loss directly to optimize the deep neural network.

Joint Unsupervised Learning (JULE) [paper] [code]

Inspired by recurrent nature of agglomerative clustering, JULE uses a convolutional neural network with agglomerative clustering loss to achieve impressive performance without the need of any reconstruction loss. In every iteration, hierachical clustering is performed on the forward pass using affinity measure \(\boldsymbol{\mathcal{A}}\) and representations are optimized on the backward pass. JULE reports excellent performance on image datasets. However it has one significant limitation-agglomerative clustering requires the construction of undirected affinity matrix which causes JULE to suffer from computational and memory complexity issues.

\[\min -\frac{\lambda}{K_{c}-1} \sum_{i, j, k}\left(\gamma \mathcal{A}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)-\mathcal{A}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{k}\right)\right)\]

Clustering Accuracy (ACC):

Deep Adaptive Image Clustering (DAC) [paper] [code]

Another approach in direct cluster optimization family, DAC uses convolutional neural network with a binary pairwise classification as clustering loss. The method is motivated from a basic assumption that the relationship between pair-wise images is binary i.e. \(r_{ij}\) = 1 indicates that \(x_i\) and \(x_j\) belong to the same cluster and \(r_{ij}\) = 0 otherwise. It also adds a regularization constraint that helps learn label features as one hot encoded features, ands the similarity \(g(x_i,x_j)\) is computed as the dot product of these label features. DAC also reports superior perfromance on benchmark datasets.

\[\begin{array}{l}{L\left(r_{i j}, g\left(\mathbf{x}_{i}, \mathbf{x}_{j} ; \mathbf{w}\right)\right)=} {-r_{i j} \log \left(g\left(\mathbf{x}_{i}, \mathbf{x}_{j} ; \mathbf{w}\right)\right)-\left(1-r_{i j}\right) \log \left(1-g\left(\mathbf{x}_{i}, \mathbf{x}_{j} ; \mathbf{w}\right)\right)}\end{array}\]

Clustering Accuracy (ACC):

Information Maximizing Self-Augmented Training (IMSAT) [paper] [code]

IMSAT learns discrete representations of data using information maximization between input and cluster assignment. It proposes Self Augmentation Training, which penalizes representation dissimilarity between the original data points and augmented ones \(T(x)\).

\[{\mathcal{R}_{\mathrm{SAT}}(\theta ; x, T(x))} {\quad=-\sum_{m=1}^{M} \sum_{y_{m}=0}^{V_{m}-1} p_{\widehat{\theta}}\left(y_{m} | x\right) \log p_{\theta}\left(y_{m} | T(x)\right)}\]

It combines mutual information constraint along with SAT scheme to define objective function as:

\[\min \mathcal{R}_{\mathrm{SAT}}(\theta ; T)-\lambda[H(Y)-H(Y | X)]\]

Clustering Accuracy (ACC):

Discussion

Benefits

  1. High Dimensionality

    Many clustering algorithms suffer from the major drawback of curse of dimensionality. Most of the algorithms rely heavily on similarity measures based on distance functions. These measures work relatively well in low dimensional data, but as the dimensionality grows, they loose their discriminative power, severely affecting clustering quality .

    Deep clustering algorithms use deep neural networks to learn suitable low dimensional data representations which alleviates this problem to some extent. Even though classical algorithms like Spectral Clustering address this issue by incorporating dimensionality reduction in their design, neural networks have been very successful in producing suitable representations from data for a large range of tasks when provided with appropriate objective functions. Therefore, deep clustering algorithms shine for their ability to learn expressive yet low dimensional data representations suitable for clustering from complex high dimensional data.

  2. End to End Framework

    Deep clustering frameworks combine feature extraction, dimensionality reduction and clustering into an end to end model, allowing the deep neural networks to learn suitable representations to adapt to the assumptions and criteria of the clustering module that is used in the model. This alleviates the need to perform manifold learning or dimensionality reduction on large datasets separately, instead incorporating it into the model training.

  3. Scalability

    By incorporating deep neural networks, deep clustering algorithms can process large high dimensional datasets such as images and texts with a reasonable time complexity. The representation space learned are low dimensional spaces, allowing other clustering algorithms to efficiently cluster large real world datasets and infer cluster information in the real time after the initial training.

Challenges

  1. Hyper-parameters

    Deep clustering models have several hyper-parameters which are not trivial to set. The major drawback of deep clustering arises from the fact that in clustering, which is an unsupervised task, we do not have the luxury of validation of performance on real data. We have to rely on benchmark datasets to evaluate the hyper-parameters and hope it translates to the real world, which seriously questions the plausibility of application of deep clustering models in the real world scenarios. This is even more worrying when we notice that all the models we discussed above generally perform very well on MNIST, but their performance may vary wildly on other datasets like Reuters.

  2. Lack of interpretability

    Although interpretability is big issue with neural networks in general, the lack of it is specially more significant in scenarios where validation is difficult. The representations learnt by deep neural networks are not easily interpretable and thus we have to place significant level of trust on results produced by the models. Therefore, deep clustering models with interpretable or disentangled representations should be developed which afford insight into what features do the representations capture and what attributes of data are the clusters based on.

  3. Lack of theoritical framework

    The majority of deep clustering algorithms we discussed above lack strong theoretical grounding. A model can be expressive and reliable without theoretical grounding, but it is often very difficult to predict their behaviour and performance in out of sample situations, which can pose a serious challenge in unsupervised setup such as clustering.

Comments